問題
次の連立不等式を解け.
解説
- (1) $\begin{cases}4x+3\le -21\\[2pt] 2x+1<3x+11\end{cases}$
- $4x\le -24\Rightarrow x\le -6,\quad 1<x+11\Rightarrow x>-10.$
よって, $-10<x\le -6$.

- $4x\le -24\Rightarrow x\le -6,\quad 1<x+11\Rightarrow x>-10.$
- (2) $\begin{cases}8-3x>2x+6\\[2pt] 5+3x>5x+9\end{cases}$
- $-5x> -2\Rightarrow x<\dfrac{2}{5},\quad -2x>4\Rightarrow x<-2.$
よって, $x<-2$.
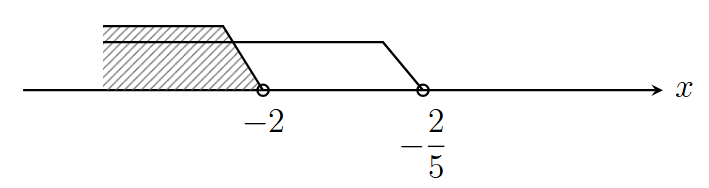
- $-5x> -2\Rightarrow x<\dfrac{2}{5},\quad -2x>4\Rightarrow x<-2.$
- (3) $\begin{cases}3x-2<4(x-1)\\[2pt] 0.3(x-1)>0.2x+0.1\end{cases}$
- $3x-2<4x-4\Rightarrow x>2,$
$0.3x-0.3>0.2x+0.1\Rightarrow 0.1x>0.4\Rightarrow x>4.$
よって, $x>4$.
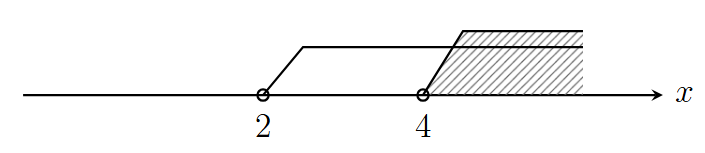
- $3x-2<4x-4\Rightarrow x>2,$
- (4) $\begin{cases}3+x\le \dfrac12(x+8)\\[6pt] 3x-5>\dfrac{x+25}{3}\end{cases}$
- $3+x\le \dfrac12x+4\Rightarrow \dfrac12x\le 1\Rightarrow x\le 2,$
$3x-5>\dfrac{x+25}{3}\Rightarrow 9x-15>x+25\Rightarrow 8x>40\Rightarrow x>5.$
よって, 解なし.
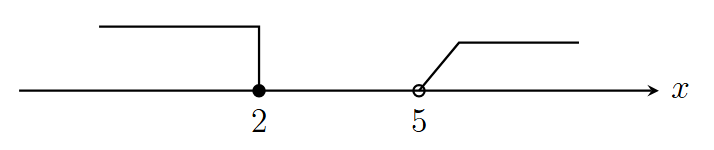
- $3+x\le \dfrac12x+4\Rightarrow \dfrac12x\le 1\Rightarrow x\le 2,$

